My friend Vincenzo recently posted up a review of academic work on clustering that he compiled while working at the University of Naples. It’s worth a look if you’re interested in the field, going from the basic methods all the way up to the latest techniques like Support Vector Clustering (which I believe you can read about in Enzo’s masters thesis).
Clustering, for those who haven’t encountered it, refers to partitioning some data into a number of groups, or clusters. It’s an unsupervised technique, unlike classification, as there aren’t any examples to learn which groups different types of data should go into. The ideal algorithms even attempt to work out how many groups there should be, but for a lot of the simpler techniques the number of clusters is an input parameter.
This can be useful for all sort of reasons, but one particular example Vincenzo gives is for guiding searches - for example a search for ‘tiger’ might give results as on a regular page, but also offer refinements for Tiger Woods, the tiger the animal, or the version of Mac OSX; allowing searchers to focus their queries on some particular grouping of results.
Probably the simplest method is the K-Means algorithm, which places k points in the data space then progressively averages them with the items around them. This is a flat clustering technique - there’s no relationship between the clusters, as opposed to (more advanced) hierarchical clustering algorithms. Below I’ve knocked up a brief implementation (download the whole source on GitHub), though for the example rather than using a whole document vector (a series of values that represents a document based on the words it contain) as you would for a real search engine, we have a set of simple 2 dimensional points.
<?php
$data = array(
array(0.05, 0.95),
array(0.1, 0.9),
array(0.2, 0.8),
array(0.25, 0.75),
array(0.45, 0.55),
array(0.5, 0.5),
array(0.55, 0.45),
array(0.85, 0.15),
array(0.9, 0.1),
array(0.95, 0.05)
);
?>Our first step is to randomly initialise the points around which we will cluster, referred to as the centroids. We try to stay inside the bounds of the data, as we know our points are going to be at the center of a circle, so we limit the rand function with the min and max. The function takes the data to cluster, formatted as above (though with any number of entries), and a value k to represent the number of clusters we want.
<?php
function initialiseCentroids(array $data, $k) {
$dimensions = count($data[0]);
$centroids = array();
$dimmax = array();
$dimmin = array();
foreach($data as $document) {
foreach($document as $dimension => $val) {
if(!isset($dimmax[$dimension]) || $val > $dimmax[$dimension]) {
$dimmax[$dimension] = $val;
}
if(!isset($dimmin[$dimension]) || $val < $dimmin[$dimension]) {
$dimmin[$dimension] = $val;
}
}
}
for($i = 0; $i < $k; $i++) {
$centroids[$i] = initialiseCentroid($dimensions, $dimmax, $dimmin);
}
return $centroids;
}
function initialiseCentroid($dimensions, $dimmax, $dimmin) {
$total = 0;
$centroid = array();
for($j = 0; $j < $dimensions; $j++) {
$centroid[$j] = (rand($dimmin[$j] * 1000, $dimmax[$j] * 1000));
$total += $centroid[$j]*$centroid[$j];
}
$centroid = normaliseValue($centroid, sqrt($total));
return $centroid;
}
/* We're expecting normalised docs */
function normaliseValue(array $vector, $total) {
foreach($vector as &value) {
$value = $value/$total;
}
return $vector;
}
?>Once we have our starting points we can then look at the main meat of the algorithm, the loop of iteratively moving and testing the centroids to find those that fit the data.
<?php
function kMeans($data, $k) {
$centroids = initialiseCentroids($data, $k);
$mapping = array();
while(true) {
$new_mapping = assignCentroids($data, $centroids);
$changed = false;
foreach($new_mapping as $documentID => $centroidID) {
if(!isset($mapping[$documentID]) ||
$centroidID != $mapping[$documentID]) {
$mapping = $new_mapping;
$changed = true;
break;
}
if(!$changed){
return formatResults($mapping, $data);
}
$centroids = updateCentroids($mapping, $data, $k);
}
}
// just a function to tidy the results up
function formatResults($mapping, $data) {
$result = array();
foreach($mapping as $documentID => $centroidID) {
$result[$centroidID][] = implode(',', $data[$documentID]);
}
return $result;
}
?>The two new functions referenced in the main loop are assignCentroids, and updateCentroids. The first just takes the current centroids and maps data to the closest one, using the absolute distance between them. This is also our stopping condition - if no data swap clusters in an iteration, we assume we’re done and exit.
<?php
function assignCentroids($data, $centroids) {
$mapping = array();
foreach($data as $documentID => $document) {
$minDist = null;
$minCentroid = null;
foreach($centroids as $centroidID => $centroid) {
$dist = 0;
foreach($centroid as $dim => $value) {
$dist += abs($value - $document[$dim]);
}
if(is_null($minDist) || $dist < $minDist) {
$minDist = $dist;
$minCentroid = $centroidID;
}
}
$mapping[$documentID] = $minCentroid;
}
return $mapping;
}
?>The second function, updateCentroids, just moves the centroid to the average of all the points that are ‘assigned’ to it. If we end up with an unassigned centroid, we simply generate some new random coordinates for it so it goes back into the pool.
<?php
function updateCentroids($mapping, $data, $k) {
$centroids = array();
$counts = array_count_values($mapping);
foreach($mapping as $documentID => $centroidID) {
foreach($data[$documentID] as $dim => $value) {
$centroids[$centroidID][$dim] += ($value/$counts[$centroidID]);
}
}
if(count($centroids) < $k) {
$centroids = array_merge($centroids,
initialiseCentroids($data, $k - count($centroids)));
}
return $centroids;
}
?>Running the whole thing gives us the following output (or a var_dump on it does anyway):
<?php
array(3) {
[0]=>
array(4) {
[0]=>
string(9) "0.05,0.95"
[1]=>
string(7) "0.1,0.9"
[2]=>
string(7) "0.2,0.8"
[3]=>
string(9) "0.25,0.75"
}
[2]=>
array(3) {
[0]=>
string(9) "0.45,0.55"
[1]=>
string(7) "0.5,0.5"
[2]=>
string(9) "0.55,0.45"
}
[1]=>
array(3) {
[0]=>
string(9) "0.85,0.15"
[1]=>
string(7) "0.9,0.1"
[2]=>
string(9) "0.95,0.05"
}
}
?>The centroids, and the natural clustering of the data, is a bit easier to see on a chart:
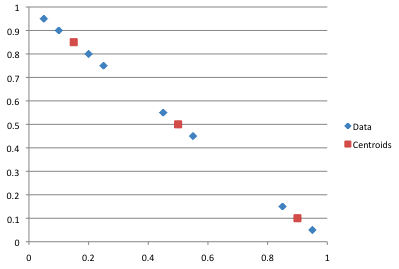
You can see in the output array that the data has clustered as we’d expect it to, but that is in part because of the random starting positions that were chosen. If they had been slightly different we might have ended up with a different partitioning of the data, one which may be less optimal. It we were being clever we could use a mix of random and intentional points - place one random, one as far away from it as possible, the next as far away as possible from that one, and so on. This can be a bit of an effort if you’ve got a lot of dimensions, but will likely result in a more reliable algorithm.
